Я - учитель математики. Школьники относятся к этому предмету неоднозначно. Кому-то этот предмет кажется скучным, кому-то сложным. Как мне современному учителю, зажечь своим предметом каждого ученика? Как раскрыть талант ребёнка?
Моя задача- научить ребёнка математике незаметно для него самого, учитывая его психологические и физиологические особенности. Именно так работает когнитивная технология, часть которой. А именно, когнитивно-визуальный подход, я использую на своих уроках.
Приёмы
- Приём «Ассоциативная разминка
На этапе изучения новой темы я провожу с учащимися практические работы для формирования визуального образа, который ассоциируется с каким-либо термином или проблемой. В когнитивной технологии он называется «визуальный якорь». В основном якоря мы создаём вместе, но иногда дети делают это самостоятельно. Их идеи бывают самые невероятные.
Я озвучиваю детям названия якорей, и необходимо угадать, с каким математическим понятием, он ассоциируется.
Переменная – хамелеон
Парабола – дерево
Уравнение – весы
Смайлик – скобки
Параллелограмм – стол
Вывод: такой приём помогает активизировать деятельность, развивает образное мышление.
- Приём « Ассоциативный образ»
«Возьмите, пожалуйста, книгу, но не открывайте её. По моей команде вы откроете книгу, в которой находится определение. Делаем паузу 10 секунд, далее закрываем глаза и книгу. Настройтесь на творчество. Не зацикливайтесь на понимании, а обратите внимание только на выделенное слово. Первое впечатление самое запоминающееся. Теперь попытайтесь нарисовать образ, который вы создали. Какие у вас образы возникли? Почему?»
Вывод: данный приём позволяет «заякорить» определённое математическое понятие и в дальнейшем при работе с ним у детей с развитым правым полушарием, возникает тот самый якорь, который ассоциируется с этим понятием.
- Приём «Визуальный якорь»
«Я вам предлагаю решить квадратное уравнение способом выделения полного квадрата.
х²+4х – 12 =0
Для того, чтобы приступить к его решению, нам необходимо вспомнить формулу сокращённого умножения квадрат суммы.
(a+b)² = a²+2ab+b²
Её легко запомнить, если представить квадрат суммы в виде квадрата со стороной а+b.»
|
|
a |
b |
|
a |
a² |
ab |
|
b |
ab |
b² |
Вывод: При использовании приёма «Визуальный якорь» создаётся естественный образ, который ассоциируется у учащихся с определённой формулой, в данном случае - это квадрат суммы.
- Приём «Ассоциативный ремикс»
«Итак, решим квадратное уравнение способом выделения полного квадрата, применив уже созданный якорь.
Алгебраический способ решения выглядит так. Сложно, не правда ли. Этот способ воспринимается учащимися тяжело. А на самом деле необходимо найти число, которое не хватает до образования того самого квадрата из «квадрата суммы»
х²+4х – 12 = 0
Перенесём -12 в правую часть уравнения, изменив, при этом знак на противоположный. И решим уравнение с помощью набора геометрических фигур.
х²+4х = 12
х²+2·2·х+2² =12+2²
х² +4х+4 =12+4
(х+2)² =16
х+2 = 4 х+2 = -4
х = 2 х = -6
А теперь, создадим визуальный якорь - квадрат. И попробуем решить квадратное уравнение с помощью геометрических фигур»
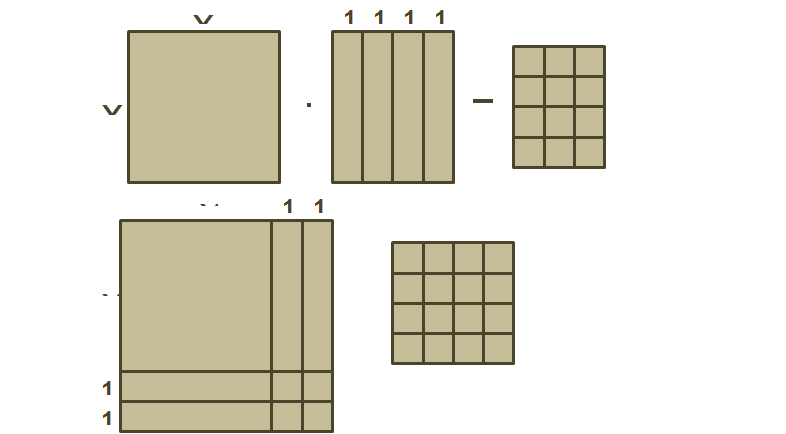
(х+2)²=16
х+2 =4 х+2 =-4
х=2 х=-6
Вывод: приём «Ассоциативный ремикс» позволяет применять на практике, созданные ранее визуальные якоря.